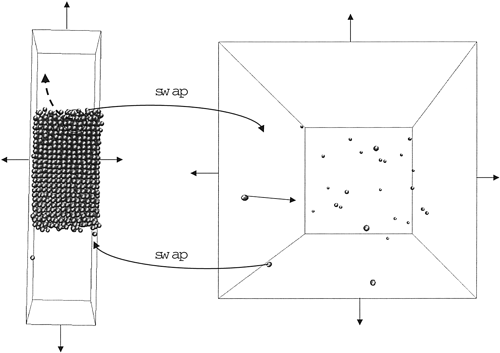
The Gibbs ensemble Monte Carlo method of Panagiotopoulos is extended to calculations of solid−vapor coexistence curves. As in the original Gibbs ensemble method, the new technique makes use of two simulation boxes that are in thermodynamic contact. However, the box that contains the solid phase is elongated along one axis and contains only a slab of solid material surrounded on both sides by vapor. Aggregation-volume-bias Monte Carlo moves are used to sample transfers from the solid to the vapor and vice versa in this box, whereas the usual particle swap moves are applied to transfers between the solid−vapor box and the other box that contains a bulk vapor phase. Volume moves for the solid−vapor box use separate displacements of individual cell lengths or of individual H-matrix elements. As one approaches the triple-point temperature from below, increased disorder at the solid−vapor interface is observed, and once the triple-point temperature is exceeded, the entire solid slab converts to a liquid. The use of configurational-bias Monte Carlo particle swap moves enables us to extend conventional Gibbs ensemble simulations of vapor−liquid equilibria beyond the triple point into the supercooled regime. Clausius−Clapeyron fits to the sublimation, and vapor pressure curves allow for the precise determination of the triple-point location. The simulation results for Lennard−Jonesium are in excellent agreement with Gibbs−Duhem integration simulations, and the results for carbon dioxide using the TraPPE force field reproduce well the experimental data (e.g., the predicted triple-point parameters are T = 212 ± 2 K and p = 430 ± 50 kPa).